tugas matematika minat

SEMESTER 1

1. 

• A. 
  2mn
• B. 
  (2mn)2
• C. 
  (3mn)2
• D. 
  (2mn)-3
• E. 
  (2mn)3

  
  

  
  

  
  

2. Gambarlah sketsa grafik dari persamaan berikut ini!

 y =$\begin{aligned}^{\frac{1}{2}}\end{aligned}$log x

3. Selesaikan sistem persamaan non linear (linear kuadrat) di bawah ini untuk solusi dalam bilangan real!

$\left.\begin{matrix} \mathrm{5x+y=7}\\ \mathrm{y^{2}=-4x}\end{matrix}\right\}$

$4.$Selesaikan sistem persamaan non linear (linear kuadrat) di bawah ini untuk solusi dalam bilangan real!

$\left.\begin{matrix} \mathrm{x=1}\\ \mathrm{4x^{2}+4y^{2}=16}\end{matrix}\right\}$

$\left.\begin{matrix} \mathrm{y=4-x}\\ \mathrm{4x^{2}+y=-5}\end{matrix}\right\}$

$5.$Penyelesaian sistem persamaan berikut ini adalah ....

$\left\{\begin{matrix} \mathrm{y=x^{2}+4x-5}\\ \mathrm{y=x^{2}+4x+3}\end{matrix}\right.$

(A) (4, 27)

(B) (2, 7)

(C) (-2, -9)

(D) (-2, -9) atau (2, 7)

(E) tidak ada penyelesaian

6. Diketahui log 3 = 0,332 dan log 2 = 0,225.maka log 18 dari soal tersebut adalah……..

a. 0,889
b. 0,556
c. 0,677
d. 0,876

Jawab:

Diket :

Log 3 = 0,332
Log 2 = 0,225

Ditanya: log 18 =…………….?

Jawaban:

Log 18 = log 9 . log 2
Log 18 = (log 3.log 3) . log 2
Log 18 = 2 . (0,332)  + (0,225)
Log 18 = 0,664 + 0,225
Log 18 = 0,889

7. Ubahlah  bentuk pangkat pada soal-soal berikut ini  ke dalam bentuk logaritma:

1.  24 = 16
2.  58 = 675
3.  27 = 48

Pembahasannya :

*Transformasikanlah  bentuk pangkat tersebut  dalam  bentuk logaritma seperti berikut ini:

Jika nilai ba = c, maka nilai untuk  blog c = a

1.  24 = 16 → 2log 16      = 4
2.  58 = 675 → 5log 675 = 8
3.  27 = 48 → 2log 48     = 7

8. Tentukanlah  nilai dari logaritma berikut ini:

• Nilai pada logaritma (2log 8) + (3log 9) + (5log 125)
• Nilai pada logaritma (2log 1/8)+(3log 1/9) + (5log 1/125)

Pembahasannya :

a.(2log 8) + (3log 9) + (5log 125)
zb.(2log 1/8) + (3log 1/9) + (5log 1/125) = (2log 2 /−3) + (3log 3 /−2) + (5log 5 /−3) = (− 3 − 2 – 3) = − 8j

Jadi, nilai yang diperoleh dari soal diatas adalah 8 dan 8j.

9. Jika Diketahui 2log 8 = a dan 2log 4 = b. maka Tentukan nilai dari 6log 14

a. 1 /2
b. (1+2) / (2+1)
c. (a+1) / (b+2)
d. (1 +a) / (1+b)

Pembahasannya:

Untuk 2 log 8     = a
=  (log 8 / log 2) = a
=  log 8 = a log 2

Untuk 2 log 4     = b
=  (log 4 / log 2) = b
=  log 4 = b log 2

Maka ,16 log 8  = (log 16) / (log68)
=  (log 2.8) / (log 2.4)
=  (log 2 + log 8) / (log 2 + log 4)
=  (log 2 + a log a) / (log 2 + b log b)
=  log2 (1+ a) / log 2( 1+ b)
=  (1+a) / (1+ b)

Jadi, nilai dari 6 log 14 pada contoh soal diatas adalah (1+a) / (1+b). (D)

10.  Nilai dari (3log 5 – 3 log 15 + 3log 9)…… ?

a. 2
b. 1
c. 4
d. 5

Pembahasannya :

(3log 5 – 3log 15 + 3log 9
= 3log ( 5 . 9) / 15
= 3log 45/15
= 3log 3
=1

Jadi nilai dari 3log 5 – 3log 15 + 3log 9 adalah 1. (B)

SEMESTER II

1. Diketahui titik A(2, 7, 8); B(-1, 1, -1); C(0, 3, 2). Jika (AB) ⃗ wakil u ⃗ dan (BC) ⃗ wakil v ⃗ maka proyeksi orthogonal vektor u ⃗ dan v ⃗ adalah ...

PEMBAHASAN:

Rumus untuk mencari proyeksi orthogonal vektor u ⃗ dan v ⃗ adalah:

Mari, kita cuss kerjakan soalnya:
Proyeksi orthogonal vektor u ⃗ dan v ⃗ adalah: 

JAWABAN: A

2. Diketahui vektor  dengan 0 < a < 8. Nilai maksimum adalah ...

a.    108
b.    17
c.    15
d.    6
e.    1
PEMBAHASAN:

    (a – 6)(a – 1) = 0
     a = 6 dan a = 1
 -   Untuk a = 6, maka:

-    Untuk a = 1, maka:

Jadi, nilai maksimumnya adalah 17.
JAWABAN: B

3.    Diketahui vektor . Jika vektor u ⃗ tegak lurus pada v ⃗ maka nilai a adalah...
a.    -1
b.    0
c.    1
d.    2
e.    3
PEMBAHASAN:

     (a – 1)(a – 1) = 0
      a = 1
JAWABAN: C

4.    Diketahui vektor-vektor  . Sudut antara vektor u ⃗   dan v ⃗ adalah ...

PEMBAHASAN:
Soal ini dapat kita kerjakan dengan rumus perkalian skalar, misalnya vektor a dan vektor b, maka perkalian skalarnya: 
Misal, sudut antara u ⃗   dan v ⃗ adalah α, maka:

JAWABAN: C

5.    
a.    -20
b.    -12
c.    -10
d.    -8
e.    -1
PEMBAHASAN:


JAWABAN: A

6.    Diketahui vektor 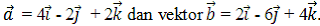Proyeksi vektor orthogonal vektor a ⃗ pada vektor b ⃗ adalah ...

PEMBAHASAN:
Rumus untuk mencari proyeksi orthogonal vektor a ⃗ dan b ⃗ adalah:

JAWABAN: B


7.    Pada persegi panjang OACB, D adalah titik tengah OA dan P titik potong CD dengan diagonal AB.
 

PEMBAHASAN:
Perhatikan persegi panjang OABC berikut:

      CP : DP = 2 : 1

JAWABAN: B

8.    
  
PEMBAHASAN:

       2(-3) + 4(m) + 1(2) = 0
       -6 + 4m + 2 = 0
       4m = 4
       m = 1

JAWABAN: B

9.    Diketahui titik P (2, 7, 8) dan Q(-1, 1, -1). Titik R membagi PQ di dalam dengan perbandingan 2 : 1 panjang (PR) ⃗ = ...
a.    √4
b.    √6
c.    √12
d.    √14
e.    √56 
PEMBAHASAN:
Kita gambarkan soal di atas dalam ilustrasi berikut:

Vektor R = ( 2 . vektor Q + 1 . vektor P ) : (2 + 1)
               = (2 ( -1, 1, -1 ) + 1 ( 2, 7, 8 )) : 3
               = (( -2, 2, -2 ) + ( 2, 7, 8 )) : 3
               = ( 0, 9, 6 ) : 3
               = (0, 3, 2)
Maka, (PR) ⃗ = (2 – 0, 7 – 3, 8 – 2)
                    = (2, 4, 6)

JAWABAN: E

10.    Agar kedua vektor  segaris, haruslah nilai x – y = ...
a.    -5
b.    -2
c.    3
d.    4
e.    6
PEMBAHASAN: 

    (x, 4, 7) = k(6, y, 14)
    (x, 4, 7) = (6k, yk, 14k)
    x = 6k
    4 = yk
    7 = 14k
    k = 7/14
    k = ½
Karena k = ½, maka x = 6k = 6.1/2 = 3, dan
yk = 4
y.1/2 = 4
y = 4 : ½
y = 8
Maka nilai x – y = 3 – 8 = -5
JAWABAN: A